How does this bear up in practice? Let’s look at dynamic impedance measurements of red LEDs in the singular and then arrayed as we propose to do here.
Examination of the published voltage versus current curves of a number of ordinary LEDs indicated that at 10mA and higher, the curves tended toward straight lines with the slope equal to the dynamic resistance. Below that current, the curvature becomes very noticeable, which is another way of saying that the device becomes nonlinear.
So one way to measure the impedance is to obtain full If-Vf curves and derive the impedance from the slope. The big advantage of that method is that the impedance at any arbitrary current can be derived; additionally, examination of the curves will give a good indication of the desired minimum current to get a nice flat, low impedance with the particular LED under consideration. However, static curves will not indicate any changes in impedance with frequency, so that will be investigated.
The method I used here was an in-circuit measure of dynamic impedance. The test circuit used is shown below:
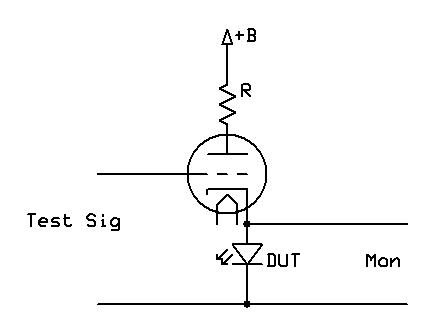
It is a basic common-cathode amplifier biased by the device under test (DUT). The circuit is fed from a variable high voltage supply and a signal generator supplies grid excitation. For the small signal tests here, the tube used was a 6SN7; the choice of tube is not terribly critical as long as it is comfortable running the desired test current. The plate resistor was 4.7k. With no signal input, the high voltage supply was adjusted for the desired idle current, in my testing, 5, 10, 15, and 20mA. Then the test signal was applied to the grid and adjusted to give the desired current swing (typically 1mA). Figure 1 For baseline comparisons between devices, an idle current of 10mA (corresponding to a 47V drop across the plate resistor) and a signal current of 1mA (corresponding to a 4.7V swing at the plate) were used. I tried quite a few, using a 1kHz sine wave as excitation. There is quite a disparity in resistances between different types or manufactures of LEDs, ranging from under 5 ohms to over 15 ohms. But the consistency between units of the same type was uniformly excellent.
The best of the lot came from a no-name bin at an electronic surplus house and measured about 4.5 ohms. I have also measured some Agilent HLMP6000s, and they were superb, just over 2 ohms. But they aren’t quite as cheap as the surplus ones…
Just to be certain that the array performed as predicted, a John Holmes version of the single-LED test jig was assembled using a triode-connected EL34 and a plate load of 220 ohms. At 80mA through the array, the AC impedance measured 4.7 ohm. That’s a cathode load we can live with. Changing the excitation to a square wave, the response of this array was seen to be well better than the rise time of my function generator. Bandwidth will not be an issue, and if you’d rather evaluate dynamic impedance using the If-Vf curves, the results will be valid to a very high frequency. And, of course, the voltage recovery at the cathode after overload will be ridiculously faster than the ear can hear. We may declare the bias design to be complete.
Two more details and we can leave the output stage. First, the size of grid-leak resistors. This is always a trade-off between wanting a large value to minimize loading of the driver stage and wanting a lower value to minimize the possibility of unwanted grid leakage current and the possibility of output tube runaway. The EL84, like most power tubes, has two specified maximum grid resistor values; for cathode biasing, a 1M value is allowed. For fixed bias, the maximum is only 300k. Naively, one might think that, since the LED array biases the tubes via the cathode, that the 1M rating would be appropriate. This turns out not to be the case. Generally, cathode bias applied via a bypassed resistor will provide some feedback near DC. So if the tube’s current starts to drift upward, the voltage across the cathode resistor will also increase, which bucks the upward current drift. That’s why we can tolerate a large grid resistance in cathode biased circuits.
The LED array, by contrast, has a nearly constant DC voltage across it independent of current, thus providing almost no DC feedback compare to the typical 100-300 ohm resistor used in cathode biasing. So we are stuck with the fixed-bias resistor maximum. But 300k isn’t too bad of a load for any reasonable driver stage. 270k is a standard value, safely within that limit, so that’s what I used.
The other detail we should attend to is the adjustment of output stage current.
Normally in a fixed-bias amplifier, the output stage idle current is adjusted via a variable negative voltage applied through the grid-leak resistor. Since like a cathode-biased amplifier the grid leaks are returned to ground, we do not have that option. And, as we have just mentioned, we do not have the luxury of DC feedback in the cathode bias circuit to take care of tube to tube variation- we must provide adjustability in a different way. Note that in pentode mode, the tubes’ screens are supplied by a DC voltage. Since the tube’s characteristics are very dependent on the screen voltage (much more so than from the plate voltage), good design practice demands that the screen voltage be regulated. And to adjust the output stage idle current, the regulator output ought to be adjustable.
For these operating conditions, the screen voltage will nominally be 280-290V or so, so we will design the regulator to be adjustable from 250V to the rated maximum screen voltage of 300V. This is not the onerous requirement that regulating the plate supply would be, due to the much lower current requirements of the screens (one more advantage of our choice of pentode mode). We can get very fancy with regulator design if that’s our inclination, but as before, I’ll let someone else do the work. And that someone is Michael Maida of National Semiconductor, who showed how to use a three-pin adjustable regulator (the LM317) in high voltage service. This is accomplished by floating the regulator by means of a high voltage bipolar transistor; a high voltage MOSFET would also work. In this case, the requirements of ultra-low noise and ultra-low source impedance are not particularly important, so we can even simplify Maida’s circuit a bit.
Our version of the screen regulator is shown here, shamelessly adapted from a Joe Curcio design:
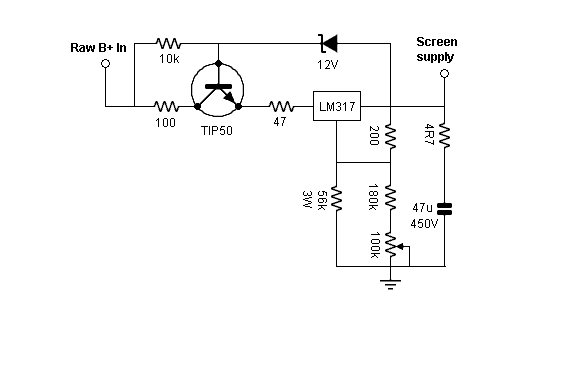
The bipolar transistor is used to limit the voltage across the LM317 to the Zener voltage less the Vbe drop of the bipolar. I have shown a 12V unit here, but this value may be adjusted slightly to accommodate parts on hand. Basically, we need enough voltage across the LM317 to keep it from dropping out of regulation, but not so much that the raw supply can’t keep up under full drive. Let’s put a few numbers to that. In the worst case, we’ll need the full 300V output that the regulated supply is capable of. At full tilt, the screen current requirement is 11mA per tube, for a grand total of 44mA. We’ll give some safety margin and design for 50mA. We will assume a 12V Zener. Working backward, if all is well, the voltage at the base of the pass transistor will be 12V higher than the output, 312V. So the voltage at the emitter is slightly over 311V because of the Vbe drop. Dropping 50mA across the combination of the 100R and 47R safety resistors, we burn up 7.5V, making the input voltage to the regulator about 303.5V (abusing our significant figures for the purpose of pedagogy). That leaves 3.5V across the regulator chip, comfortably above its dropout voltage.
Turning back to the bipolar pass transistor, we need to know that it won’t be challenged. That part will depend on the raw supply for the output stage B+. With the particular transformer used in my build (a salvaged unit from the same SCA35 which gave its all to provide us with output transformers), the full-load voltage is 320V; no-load is closer to 350V. This means that there is always at least 8-9V to keep the bipolar happy. The supply should work. We do need to check the value of the supply resistor for the Zener and transistor base. Under worst-case, the transistor will need to supply 50mA. So if the transistor has an hfe of 50, we’ll need to allow for a milliamp of base current. The Zener will want at least a milliamp of its own, so we’re obliged to supply at least 2mA to that portion of the circuit. So, using Ohm’s Law, we can calculate a safe value for the Zener’s supply resistor; 10k will work fine.
I’ve done one small trick here in the regulator’s adjustment leg: running DC through a trim pot wiper can cause long-term reliability issues. The lower the DC, the better. That’s the reason for the rather odd looking paralleled resistor combination used to set the regulator output voltage. With the values shown, the regulator output should be adjustable from 250-300V, which should accommodate most makes of EL84. Despite the relief afforded the trimmer, it still does carry some current, so don’t use a wimpy one.
Depending on your access to matched output tubes and degree of perfectionism, you may wish to use separate regulators for each channel. I had some matched quads from one of my dealers, so I just used a single regulator (and adjustment) for all output tubes. If you use matched pairs, two regulators would be best. If you really want to groove, you could use a separate regulator for each output tube, but that’s truly overkill.
In order to monitor the output stage current, we will place a small resistor (1.0 ohms) in series with each LED array. With a millivoltmeter connected across it, one can directly read the cathode current in milliamperes. The resistor does compromise the low cathode impedance slightly, but at a total of 5R7 with the resistor (as opposed to 4R7 without it), the compromise is tolerable. If this worries you at all, feel free to devise a system that shorts the resistor except during measurement; a pluggable link, a phone jack with an integral switch, a separate switch, or even a soldered piece of wire will all work. My feeling is that if this resistor troubles you, you probably straighten your bow-tie using a laser level.
And just for grins, I added some 4R7 resistors in series with each LED string, which allowed me to see if any of the strings were hogging current or slacking. Turns out that the currents all fell into a 10% window. And the resistors help equalize that at the minor expense of something less than one more ohm of cathode impedance.
The output stage is adjusted for a cathode current of 85mA or so for each channel (two tube total). This burns about (0.085A)(320V) = 27.5W per output pair, or slightly over 13W per tube at idle. That’s comfortably below the maximum rating.

Hello SY,
Excellent article. Very well written; even a chemical engineer can understand most of it. And other than the important subject of coconut migration, the Holy Grail is well covered too:)
I do have a question though. You write: “The output stage is adjusted for a cathode current of 85mA or so for each channel (two tube total). This burns about (0.085A)(320V) = 27.5W per output pair, or slightly over 13W per tube at idle. That’s comfortably below the maximum rating.”
The Mullard data sheet describes the EL84 as a 12 watt tube. How, sir, can this be described as below the max rating?
BTW, I believe the power supply drawing is missing the line from the driver power transformer center tap to ground.
Thanks
Dave
Dave, thanks for catching the misprint in the schematic!
The key to the power question is the difference between plate current and cathode current. The latter also includes the screen current. So the plate dissipation is actually within bounds once you account for that.