The Bass Section
Ok, I’m going to say something heretical- in this speaker, renowned for incredible bass, the bass is compromised. The Foster 1259 12″ driver has a very strong motor and can pump a lot of air; the designers chose to mount it in a very well-damped sealed enclosure with multiple chambers. This yields a very tight and well-defined bottom end, with the woofer rolling off gracefully, albeit not at as low a frequency as it could. The slight limitation on bass extension keeps the speaker box volume relatively reasonable, though still not exactly tiny, at just under 3 cubic feet.
Now as compromises go, this is a reasonable one; the woofer will handle lots of power and be difficult to bottom. There will be no tendency to boom with casual placement and a -3dB point just below 30Hz isn’t too shabby! A major contribution to this clean, well-defined bass is the superbly inert cabinet, and that gets prohibitively difficult to manufacture if the cabinet were to be made larger in the interests of extension. As it is, the enclosures weigh over 120 pounds because of the heavy construction and extensive bracing.
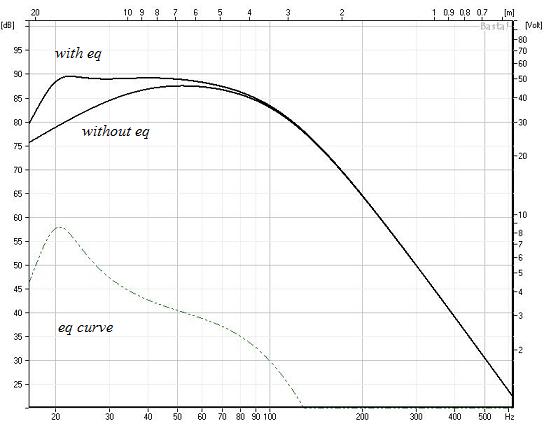
The curve below marked “without eq” shows the response of the 1259 driver in the M3.3 cabinet.
As one may surmise from the titles on the other curves, I’m heading toward shifting the compromises around. For a speaker that will primarily be handling music, we can throw bottom-octave caution to the wind and use some electronics to compensate for the bass roll-off and get a bit more extension. Again, this is an advantage of biamping- what would be a huge and impractical passive EQ network with about a hundred pounds of iron and a bank of capacitors the size of a suitcase is a piece of cake to do actively with a few ICs.
The eq curve shown is not exactly complete, it’s just the closest I can model in Basta. But it does show the effect of adding 10dB of boost at about 20-21 Hz. The “real” eq curve will have a broad hump at about 35 Hz, so it won’t show the broad dip of the modeled curve.
The actual target eq curve is shown here:
This is pretty easy to implement with some op-amps or digitally.
Practicalities: Bass section
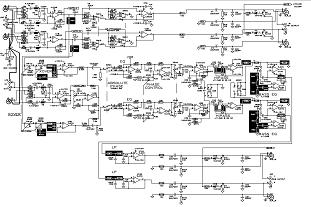
A very elegant way to do the required equalization is to modify one of the X series electronic crossovers from NHT. The commercial versions were the X1 and X2- these crossovers are very similar, but have some of the boundary equalization and LF highpass filtering shifted around a bit. With some effort, they can be found new, in which case what I describe here voids the warranty, and does so with extreme prejudice. However, X crossovers are pretty easy to find on EBay, Audiogon, and other For Sale sites. Figure to pay $150-$200 for one in good condition. For your money, you get a very nice case, great control flexibility, variable phase, and a built-in reasonably competent high pass filter for the upper section. Inputs and outputs are available balanced (XLR) or unbalanced (RCA). The schematics and parts numbering for both models is the same; only a few values are different. Likewise, either can be converted to run the M3.3 project, providing the proper EQ to the 1259 woofer.
Here is a schematic indicating the parts which are different between the crossover models and a table showing the values for the X1, X2, and the X conversion for the M3.3: (click to enlarge)
| Component | X1 | X2 | X3.3 | |
| R53, R54, R57, R58 | 3k0 | 1k0 | 1k0 | |
| R133, R136 | 27k | open | open | |
| R87, R96 | 2k2 | 29k4 | 29k4 | |
| R89, R94 | 20k | 29k4 | 29k4 | |
| R84, R85 | 200k | 75k | 200k | |
| R83, R86 | 2k2 | 36k | 6k9 | |
| R90, R91, R92, R93 | 2k7 | 14k3 | 14k3 | |
| R97, R98, R99, R100 | 5k1 | 5k1 | 430R | |
| C27, C28 | 220n | 470n | 470n | |
| C26, C29 | 100n | 220n | 220n | |
| C44, C49 | 220n | 100n | 100n | |
| C46, C47 | 10u | 1u | 1u | |
The schematic is pretty straightforward, and a block diagram may be found in the X series owners’ manuals, available at NHT’s website. If you want to build it yourself, there’s a lot of sections you don’t need; you can lift chunks out of the schematic and piece them together into something less versatile, but perfectly suitable for this project.
The snooty audiophile, like me, will avoid using the high-pass section of the X3.3 and will build his (I use the gender deliberately) own 2nd order Butterworth at 110Hz. In my case, I used a tube buffer similar to the Heretical. But for the other 99% of the world, the circuit in the X3.3 is Good Enough.
Tuning
Here’s where you’ll want to get a mike and some appropriate software (REW, Arta, SynRTA, or the like). The goal is to set the “Boundary EQ” control for the flattest bass just above cutoff (that will be near the “+3dB” setting of that knob), the “Master Gain” control to match the woofer’s output to the rest of the system, and the phase and low-pass frequency controls to get the 110Hz crossover as seamless as possible when measured near where you’ll be sitting (probably normal polarity, 20-30 degrees of phase, and the low-pass frequency anywhere from 110-130 Hz).
Proof of the Pudding
How does it all work in practice? Here’s a spectrum, using the excellent REW software, of the in-room response of the stereo pair at my listening position (about 2.5 meters). 1/48th octave, so no makeup. The SPL scale is relative, not calibrated- SPL at the listening position was probably about 85dB or so. 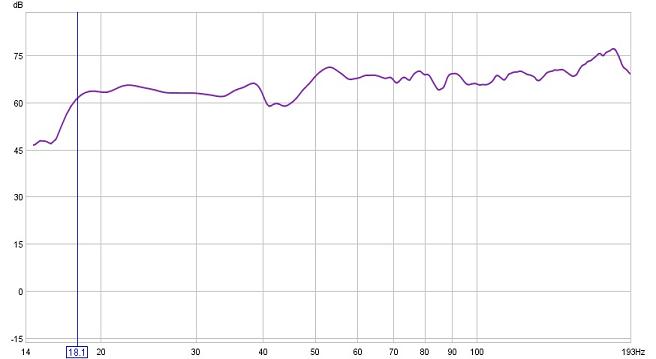
There are a few things of note. The bad news is the glitch at about 40 Hz and the 3dB shelf-down of response below that point. This is a nice measure of the point at which the plasterboard room boundaries cease to be reflective and the walls “breathe” with the bass. Yow! Well, I can’t blame the speakers for that. The good news is our 110 Hz crossover point- it’s seamless! I can wave the mike around for a foot or so without seeing any sort of notch or peak there. Given the large driver separation, that’s pretty damned impressive. More good news is that the Allison dip in the 160Hz range is entirely absent. Credit the hump in the mid-bass driver’s response, along with careful attention to the phase through the crossover range.
The faster-than-textbook HF rolloff of the midbass driver also contributes to the impressive midbass, compensating for baffle loss and flattening out the response through its passband.
And I hesitate to mention it, but… notice the bass -3dB frequency?
Subjectively, the bass seems almost casually even and well-defined. There’s no sense of the transition between the various drivers, images are solidly fixed. Effortless and natural. The boom-dee-boom source material does all the shaking and rattling you’d want, but it’s the ease and naturalness of “ordinary” music that really stands out.
Acknowledgements
Obviously, Jack Hidley and crew from Audio Consulting Services are the real brains behind this. All I’ve done is document it and try to put some logic behind it that dimwits like me can understand. If there’s wrong stuff in here, it’s my fault, not theirs.
Updates (February 2011)
Since the time I originally wrote this, life has gotten much better. The ridiculously cheap and effective Behringer DCX2496 makes this project a particularly easy one. The passive high pass filter for the woofers is removed. The bass amp is run with a L-R 24 low pass at 110 Hz, an18 Hz Butterworth high-pass, and 6dB of EQ at 20 Hz. The upper section is modified as per this article and filtered with a Butterworth 2nd order high-pass at 110 Hz. Delay of about 1.5ms. Easy peasy! In my system, the Behringer is fed digits from my computer into Channel A, then the outputs go to a 6 channel Heretical preamp (2 extra channels for my other subwoofers, not part of this project), which in turn feeds the power amps.
The Heretical helped with the output gain situation (a common problem for consumer-level systems interfacing with pro-level gear), but ultimately, I just ripped out the Behringer’s output section and substituted Jan Didden’s passive RC balanced output, perfect for the Heretical’s input transformers. I am quite happy with the sound.